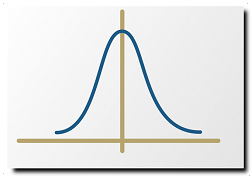
Uncertainty
Uncertainty is the range of measurements variation in relation to the same reference.
So taking an average of N measurements, the uncertainty is how far someone is from the true mean.
Test here the uncertainty calculator in the
calibration certificate generator online.
Easy alternative here:
Uncertainty Calculator.
To explain better, let’s think about a measurement which was made in three readings.
In this way, the average of these three measurements, the calculator can have a good result.
But if we take the average of 5 readings the average will be better.
Likewise, if we calculate from 100 values it will be even better and closer to the real average.
The calculation formula of the expanded uncertainty is greater than the standard deviation, with a percentage of approximately 95%.
Calculator formulas contain metrology-based details.
The calculator of calibration has
Uncertainty and
Error.
The error is the difference between the standard reference and the measured instrument. The uncertainty is just the range of variation.
Keeping that in mind, the more measurements we do, the closer to the true average my result will be.
Therefore, the more readings, the lower the uncertainty of the mean.
But the references of the standards, used in the calibration of the values to compare the measure, also have an uncertainty.
This propagation of uncertainty calculation is also associated with the uncertainty of the instrument to be measured.
The propagation calculator uses formula based on standard deviation, but expanded to a higher percentage.
The propagation of errors are also important for the calculator of deviation of numbers.
Some uncertainty calculations were made with the uncertainty principle, through Heisenberg formula.
You can understand the basic concept of uncertainty. But this matter does not end there.
There is still a lot of concept associated with measurement uncertainty.
A tool that helps a lot to make these calculations is a calibration and metrology software.
With it you will be able to meet the standards required in the market.
Not to mention the fundamental quality and practicality for calibration and metrology services.
Uncertainty is calculated with the degree of freedom.
Calculate
Degree of freedom
The degree of freedom is identified by the Greek letter:

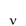
Therefore, we consider the number of readings (
N ) to calculate the degree of freedom.
The number of dimensions is also considered. Generally, for simple measurements (with only 1 dimension) we use the formula:
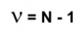
The calculator includes the degrees of freedom, as well as the coverage factor.
The k factor is used for extended uncertainty in the calculator's formula.
Combined uncertainties can also be used from the calculator to add information to the final result.
Calculate
Calculation
The measured values, whose uncertainties are calculated, are comparable with reference measurements.
The calculation of the measurements average, indifferent instruments, can show that there are a variety of values in relation to the average itself.
The data is verifiably monitored, where the information is officially provided on the instrument, it can be a digital display monitor, or it can be an analog pointer.
In addition to resolution, and instrument divisions, sometimes the values are not repeated.
They are not necessarily stable. The evaluations show that eventually the readings vary according to some influences.
Test here the uncertainty calculator in this
Calibration Online.
The elements that cause these uncertainties have a wide range of possibilities.
Therefore, the uncertainty calculation must be used, to sum with the calculated error of the instrument, in relation to the reference standard.
The settings, performed in the calibration procedure, must be defined according to the equipment’s characteristics, and also, with its area of use.
Uncertainty calculation formula can gather standard deviation with t-Student.
Generally, in the end, the degree of uncertainty is 95.45%.
Another important factor is the curve. It can be normal curve, rectangular curve, triangular curve, etc.
Interference
In addition to the mean, the uncertainty is also influenced by calculating the uncertainty of the reference standard.
The uncertainty of the standard influences the final calculation.
The reference measures also have uncertainty, so they are also associated in the correlations with the results in parallel.
Another item, which changes, and generally increases uncertainty, is the instrument’s resolution.
The resolution, or division, shows that the measurement has a minimum acceptable value.
Therefore, verification is highly dependent on this information as well.
Applicable directly in the calculator.

But in addition to
instruments that measure length, there are, for example,
pressure and
temperature instruments.
There are actually several
quantities or
units of measurement involved.
Some units can be millimeter, meter, inch, ampere, temperature, pressure, etc.
So the measuring instruments and untis may vary.
But it depends on the magnitude of what you want to measure.
Everything you measure on an instrument is called a measurand, with the specific unit.
At the sametime, there are a number of
errors in relation to the measurement action.
Thus, these errors involved are related to the measurement operation.
Errors can also be influenced by location. An example is the ambient temperature or air pressure itself.
You’ve seen some influences, right? Now let’s separate them into two groups:
Unknown
Known (
uncertainty and
error ).
Unknown influences arefound by statistical methods.
Already the known influences are grouped to the error through mathematical methods.
The uncertainty calculator is also performed according to some defined standards in the field of calibration and metrology.
Average value
To improve measurement you need to measure more than once.
And so, you will have an average of the measurements.
In this case, you can use from 3 to as many readings as necessary.
In the above formula the number of readings used in a measurement is identified by the letter
N.
The average is nothing more than the sum of readings divided by the number of readings performed.
In the next posts we will talk about the measurement concepts. So that you know these concepts, which are fundamental.
When you are familiar with the concepts of calibration and measurement, it becomes easy to use the calibration software.
Calibration informs which errors and uncertainties of the instrument numbers through the calculator.
Thus, you guarantee the desired quality and compliance with technical standards.
Monitoring Measurement is very important for monitoring.
The variables are gradually usable for interpretation of results.
Measurements can be based on various types of units.
It can be mm (millimeter), V (Volt), bar (Pressure), °F (temperature), etc.
Applicable items are scalable. The bases must be viable for each type of scope.
Instruments that perform measurements have displays or pointers.
This exposed information is official, according to the instrument.
But calibration must be performed, which is the comparison of values against the standard.
Actions must be precisely feasible, so that the guidelines received are tolerable.
That’s why calibration is very important to trust the instrument measurement.
Questions about uncertainty calculator:

Calibration certificates contain instrument values with calculator results based on metrology
The bases used for measurements vary widely.
In electronic instruments, thenumber of steps to generate the results can sometimes be large.
But the final result, presented by the monitor, must be considered the official measurement.
When the instrument is dimensional, for example, a tape measure or caliper, and does not have an electronic monitor, the fixed indications of the measurements are defined in the instrument itself.
They are verifiable against a nominal standard. For example, blocks with defined sizes.
They are evaluated individually.
To ensure that the reference, for example in millimeters or inches, is relatively adherent to the standard.
This also according to the originality of the base related to the unit.